这就是BZOJ挨个做题的下场吗
群的定义
对于二元组 \((G,\ \circ )\) 其中 \(G\) 是一个集合,$$ 是一个二元运算,若满足以下性质,则称 \(G\) 是 $$ 下的群 * 封闭性: \(\forall \ a,\ b \in G, \ a\circ b \in G\) * 交换律: \(\forall \ a,\ b,\ c \in G,\ a\circ b\circ c\ =\ a\circ (b\circ c)\) * 单位元: \(\exists \ e\ \in G,\ \forall\ a\ \in G,\ a\circ e\ =\ a\) * 逆元: \(\forall \ a\ \in G,\ \exists\ a^{-1}\ \in\ G,\ a\circ a^{-1} = e\)
比如,复数集合 \(C\) 是二元运算 \(+\) 的群,即加法群
置换群
定义 \(G\) 为 \(S = \{ 1,\ 2,\ 3,\ 4,\ ...\ ,\ n \}\) 上双射构成的集合,并定义二元运算 \(\circ\) 满足 \((f\ \circ\ g)[x] = f(g(x))\),若保证运算 \(\circ\) 对于 \(S\) 封闭,则称 \(G\) 是运算 \(\circ\) 的置换群,且这种双射称为置换,通常以这种形式表示 \[\begin{bmatrix} 1&2&3&{\cdots}&n\\\\ {a_1}&{a_2}&{a_3}&{\cdots}&{a_n}\\ \end{bmatrix}\]
其中置换
\[\begin{bmatrix} 1&2&3&{\cdots}&n\\\\ {1}&{2}&{3}&{\cdots}&{n}\\ \end{bmatrix}\]
为 \(G\) 的单位元
其中
\[\begin{bmatrix} {a_1}&{a_2}&{a_3}&{\cdots}&{a_n}\\\\ 1&2&3&{\cdots}&n\\ \end{bmatrix}\]
为 \(G\) 的逆元
同时,我们定义:
\(E_i\) 表示元素 \(i\) 经过 \(G\) 的诱导下可以得到的元素集合,即等价类
就是置换形成的有向图的环·
\(Z_i\) 表示使元素 \(i\) 为不动点的置换的全体所构成的集合
Burnside 引理
设 \(G\) 是作用在 \(S = \{1,\ 2,\ 3,\ \cdots,\ n\}\) 的置换群,则对于等价类 \(E\) 的个数 \(l\) 有
\[l\ =\ \frac{1}{|G|}\sum_{g\ \in\ G}D(g)\]
其中 \(D(x)\) 表示置换 \(x\) 中的不动点的数量
### 证明
引理
\[\sum_{i=1}^n|Z_i| = \sum_{g\ \in\ G}D(g)\]
自己口胡一遍就行了
\(\sum_{i=1}^n|Z_i|\ =\ \sum_{i=1}^n\sum_{g\ \in \ G}[i == a_i][a_i\ \in g]\ =\ \sum_{g\ \in \ G}\sum_{i=1}^n[i == a_i][a_i\ \in g]\ =\ \sum_{g\ \in \ G}D(g)\)
引理
\[\forall\ k\ \in\ S,\ |E_k||Z_k|\ =\ |G|\]
设 \(E_k\ =\ \{a_1,\ a_2,\ a_3,\ \cdots,\ a_{|E_k|} \},\ a_1\ =\ k\)
由 \(E_k\) 的定义知,\(\exists\ p_i\ \in\ G,\ p_i(a_1)\ =\ a_i\)
于是构造 \(Z_kp_i\ =\ \{\pi\circ p_i\ |\ \pi \in\ Z_k\}\)
对于 \(Z_kp_i\) 具有以下性质
\[|Z_kp_i|\ =\ |Z_k|\]
\(\because \pi_1\circ p_i\ =\ \pi_2\circ p_i \rightarrow\ \pi_1\ =\ \pi_2\ \therefore\ \pi_1\ \ne\ \pi_2\ \rightarrow \pi_1\circ p_i\ \ne\ \pi_2\circ p_i\)
结合下一条性质感性理解
\[Z_kp_i\ \cap\ Z_kp_j = \varnothing\ (i\ \ne\ j)\]
\(\because\ Z_kp_i(a_1)\ =\ a_i,\ Z_kp_j(a_1)\ =\ a_j\ \therefore\ p_i(a_1)\ \ne\ p_j(a_1)\)
\[G\ =\ Z_kp_1\ \cup\ Z_kp_2\ \cup\ Z_kp_3\ \cup\ \cdots\ \cup\ Z_kp_{|E_k|}\] 首先,显然
\(Z_kp_1\ \cup\ Z_kp_2\ \cup\ Z_kp_3\ \cup\ \cdots\ \cup\ Z_kp_{|E_k|}\ \subseteq G\)
\(\forall\ p\ \in\ G,\ p(a_1) = a = k\rightarrow a\ \in \ E_k\),设 \(a = a_j\)
\(\because\ p\circ p_j^{-1}(a_1)\ =\ p_j^{-1}\circ p(a_1)\ =\ a_1\)
\(\therefore\ p\circ p_j^{-1}\ \in\ Z_k,\ p\ \in\ Z_kp_j\)
\(\ \ \ \ G\ \subseteq\ Z_kp_1\ \cup\ Z_kp_2\ \cup\ Z_kp_3\ \cup\ \cdots\ \cup\ Z_kp_{|E_k|}\)
\(\therefore\ G\ =\ Z_kp_1\ \cup\ Z_kp_2\ \cup\ Z_kp_3\ \cup\ \cdots\ \cup\ Z_kp_{|E_k|}\)
综合各项性质
\(|G|\ = \sum_{i=1}^{|E_k|}|Z_kp_i|\ = \sum_{i=1}^{E_k}|Z_k|\ = |E_k||Z_k|\)
综上
\(\frac{1}{|G|}\sum_{g\ \in\ G}D(g)\ = \frac{1}{|G|}\sum_{i=1}^{n}|Z_i| \ = \frac{1}{|G|}\sum_{i=1}^l\sum_{j\ \in\ E_i}|Z_j| \ = \frac{1}{|G|}\sum_{i=1}^l|G|\ = l\)
例题
一正方形分成4格,2着色,求方案,其中,经过转动相同的图象算同一方案
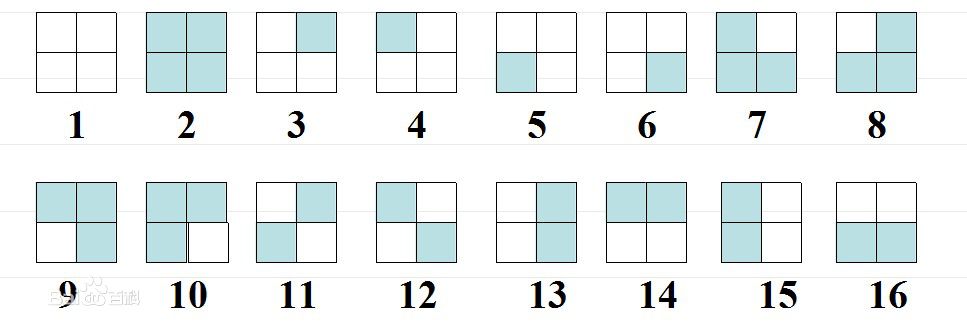
设 \(G\ =\ \{a_1,\ a_2,\ a_3,\ a_4\}\) 分别代表顺时针 \(0^{\circ}\) ,\(90^{\circ}\) ,\(180^{\circ}\) ,\(270^{\circ}\)
由题意得
\[a_1\ = \begin{bmatrix} 1&2&3&4&5&6&7&8&9&10&11&12&13&14&15&16\\\\ 1&2&3&4&5&6&7&8&9&10&11&12&13&14&15&16\\ \end{bmatrix}\]
\[a_2\ = \begin{bmatrix} 1&2&3&4&5&6&7&8&9&10&11&12&13&14&15&16\\\\ 1&2&6&3&4&5&10&7&8&9&12&11&16&13&14&15\\ \end{bmatrix}\]
\[a_3\ = \begin{bmatrix} 1&2&3&4&5&6&7&8&9&10&11&12&13&14&15&16\\\\ 1&2&5&6&3&4&9&10&7&8&11&12&15&16&13&14\\ \end{bmatrix}\]
\[a_4\ = \begin{bmatrix} 1&2&3&4&5&6&7&8&9&10&11&12&13&14&15&16\\\\ 1&2&4&5&6&3&8&9&10&7&12&11&14&15&16&13\\ \end{bmatrix}\]
由Burnside引理得
\[l\ =\ \frac{1}{4}\times (16+2+4+2)\ =\ 6\]
Polya 定理
我们考虑染色问题,\(S\) 大小是指数级的,无法枚举,所以产生了Polya定理
引入循环的概念
约定一个记号
\[(a_1\ a_2\ a_3\ \cdots\ a_n)\ =\ \begin{bmatrix} {a_1}&{a_2}&{a_3}&{\cdots}&{a_n}\\\\ {a_2}&{a_3}&{a_4}&{\cdots}&{a_1}\\ \end{bmatrix}\]
循环可以理解为压缩表示的置换,对于循环内的数没有先后之分
一个十分显然的结论,一个置换可以表示成若干个不相交循环的组合
例如
\[(a_1\ a_2\ a_3)(a_4\ a_5)\ =\ \begin{bmatrix} {a_1}&{a_2}&{a_3}&{a_4}&{a_5}\\\\ {a_2}&{a_3}&{a_1}&{a_5}&{a_4}\\ \end{bmatrix}\]
设 \(G\) 是作用在 \(S = \{1,\ 2,\ 3,\ \cdots,\ n\}\) 的置换群,我们需要对 \(n\) 染 \(m\) 种颜色,则对于等价类 \(E\) 的个数 \(l\) 有
\[l\ =\ \frac{1}{|G|}\sum_{g\ \in\ G}m^{C(g)}\]
其中 \(C(x)\) 表示置换 \(x\) 中的不相交循环的数量
证明
对于每个循环都对应的是该置换的不动点,我们只要把循环内的数染成相同颜色即可,即 \(m^{C(g)}\) 个
人类本质
一正方形分成4格,2着色,求方案,其中,经过转动相同的图象算同一方案
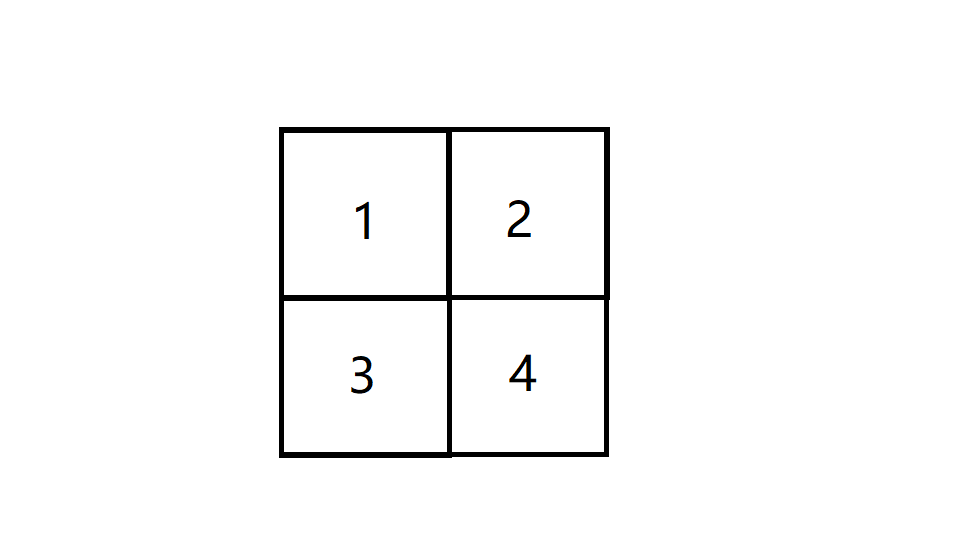
设 \(G\ =\ \{a_1,\ a_2,\ a_3,\ a_4\}\) 分别代表顺时针 \(0^{\circ}\) ,\(90^{\circ}\) ,\(180^{\circ}\) ,\(270^{\circ}\)
由题意得
\[a_1\ =\ (1)(2)(3)(4)\]
\[a_2\ =\ (1\ \ \ 2\ \ \ 3\ \ \ 4)\]
\[a_3\ =\ (1\ \ \ 3)(2\ \ \ 4)\]
\[a_4\ =\ (1\ \ \ 2\ \ \ 3\ \ \ 4)\]
由Polya定理得
\[l\ =\ \frac{1}{4}\times (2^4+2^1+2^2+2^1)\ =\ 6\]
P4980 【模板】Polya定理
群论真是人类的智慧