CTime_Pup_314

不能再颓废了

0%

52709102 AGC004

发表于 更新于 分类于 阅读次数： Valine：

Colorful Slimes

有 \(2\) 种操作，花费 \(a_i\) 秒，直接获得颜色 \(i\) 和花费 \(x\) 秒，使得之前获得的颜色 \(i\) 全部变为颜色 \((i + 1)\ mod\ n\)，求收集到 \(0\) 到 \(n-1\) 所有颜色的最短时间

了解题意后，我们发现，每种方案的 \(2\) 操作一定取决于作用二操作次数最多的颜色，所以枚举 \(2\) 操作，滑动窗口最小值查询即可 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cctype>
using namespace std;
typedef long long int64;
inline int read(int f = 1, int x = 0, char ch = ' ')
{
    while(!isdigit(ch = getchar())) if(ch == '-') f = -1;
    while(isdigit(ch)) x = x*10+ch-'0', ch = getchar();
    return f*x;
}
const int N = 4e3+5;
int n, x, a[N], q[N], l, r;
int64 ans;
int main()
{
    n = read(), x = read(); 
    for(int i = 1; i <= n; ++i) a[i] = read(), a[i+n] = a[i];
    for(int k = 0; k < n; ++k)
    {
        int64 s = 1ll*k*x; l = 1, r = 0;
        for(int i = 1; i <= k; ++i)
        {
            while(l <= r&&a[q[r]] >= a[i]) --r;
            q[++r] = i;
        } 
        for(int i = k+1; i <= n+k; ++i) 
        {
            while(l <= r&&i-k > q[l]) ++l;
            while(l <= r&&a[q[r]] >= a[i]) --r; 
            q[++r] = i; s += a[q[l]];
        }
        ans = k?min(s, ans):s;
    }
    printf("%lld\n", ans);
    return 0;
}

AND Grid

给定一个网格图，有些位置已经被涂色，要求构造两个相同大小的网格图，并且在上面涂色，需要保证颜色四联通，满足这两个网格的涂色部分的重合位置恰好是给定的网格图的涂色位置

这道题保证边界无颜色，所以只需要行按照奇偶染色，最后一边染开始的一列，一边染结束的一列保证联通即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <cstdio>
#include <cctype>
using namespace std;
inline int read(int f = 1, int x = 0, char ch = ' ')
{
    while(!isdigit(ch = getchar())) if(ch == '-') f = -1;
    while(isdigit(ch)) x = x*10+ch-'0', ch = getchar();
    return f*x;
}
const int N = 5e2+5;
int n, m;
char s[N][N], a[N][N], b[N][N];
int main()
{
    n = read(), m = read();
    for(int i = 1; i <= n; ++i) scanf("%s", s[i]+1);
    for(int i = 1; i <= n; ++i) 
        for(int j = 1; j <= m; ++j)
            a[i][j] = b[i][j] = s[i][j];
    for(int i = 1; i <= n; ++i) a[i][1] = b[i][m] = '#';
    for(int i = 1; i <= n; ++i)
        for(int j = 2; j < m; ++j)
            i&1?a[i][j] = '#':b[i][j] = '#';
    for(int i = 1; i <= n; ++i) printf("%s\n", a[i]+1); puts("");
    for(int i = 1; i <= n; ++i) printf("%s\n", b[i]+1);
    return 0;
}

Teleporter

给定一个基环内向树，修改尽可能少的出边，使得每个点到 \(1\) 号节点都可以经过 \(k\) 条边到达

显然，我们需要 \(1\) 号点自身连自环，之后就变成了 [HNOI2003]消防局的设立 随便做一下就好了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cctype>
#include <queue>
using namespace std;
inline int read(int f = 1, int x = 0, char ch = ' ')
{
    while(!isdigit(ch = getchar())) if(ch == '-') f = -1;
    while(isdigit(ch)) x = x*10+ch-'0', ch = getchar();
    return f*x;
}
const int N = 1e5+5;
struct Edge
{
    int next, to;
    Edge(int next = 0, int to = 0):next(next), to(to) {};
}edge[N];
int tot, head[N];
void add(int x, int y) { edge[++tot] = Edge(head[x], y); head[x] = tot; }
int n, m;
int ac[20][N], d[N], cov[N], ans, fa[N];
void dfs(int x)
{
    d[x] = d[fa[x]]+1; for(int i = 1; i < 20; ++i) ac[i][x] = ac[i-1][ac[i-1][x]];
    for(int i = head[x]; i; i = edge[i].next) dfs(edge[i].to);
}
void cover(int x)
{
    if(cov[x]) return; cov[x] = 1;
    for(int i = head[x]; i; i = edge[i].next) cover(edge[i].to);   
}
priority_queue<pair<int, int> > q;
int main()
{
    n = read(), m = read();
    for(int x = 1; x <= n; ++x) fa[x] = read();
    for(int x = 2; x <= n; ++x) add(ac[0][x] = fa[x], x);
    ans += fa[1] != 1; dfs(1);
    for(int x = 1; x <= n; ++x) q.push(make_pair(d[x], x));
    while(q.size())
    {
        int x = q.top().second, p = x; q.pop();
        if(cov[x]||d[x]-d[1] <= m) continue;
        for(int i = 19; ~i; --i) 
            if(d[x]-d[ac[i][p]] < m&&ac[i][p]) p = ac[i][p];
        cover(p); ++ans;
    }
    printf("%d\n", ans);
    return 0;
}

Salvage Robots

有一个棋盘，每个格子有机器人，空格和出口三者之一 ，每次可以命令所有机器人向上下左右中的某个方向移动一格，如果它超出了棋盘的边界或到了出口的位置就会消失，求机器人到出口的最多数量

很自然地想到把出口和其可以移动的范围替代移动机器人，然而设计的 \(DP\) 具有会算重，之后就看了官方题解

不妨设 \(f_{l,r,d,u}\) 表示出口曾经向左走了 \(l\) 格，向右走了 \(r\) 格，向上走 \(d\) 格，向下走了 \(u\) 格，这个范围内遇到的机器人的最大数量，如图

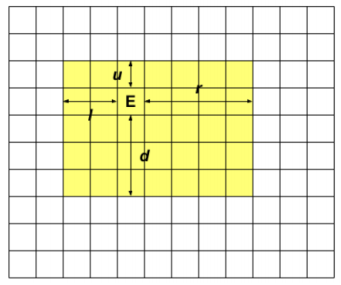状态设计

图中的黄色区域就是机器人曾经的移动范围，在这个移动范围内的机器人取舍情况已经被计算好了

接着，我们标注一下曾经有过这个移动范围的前提下，它不能走的网格

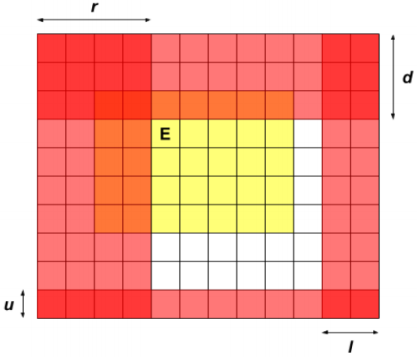禁止节点

我们发现只要向白色部分转移即可，而对于红黄相间的部分的取舍之前已经取舍过了，只有红色的部分就是走不到的部分

转移如下

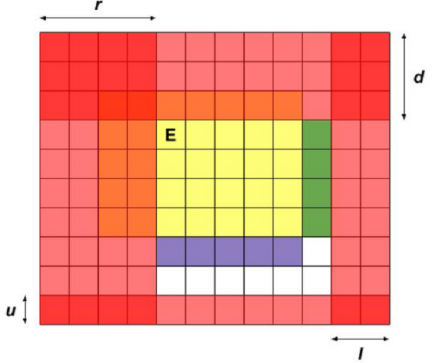转移

移动范围扩大，在加上相应颜色区域的机器人数量即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <cstring>
#include <cctype>
#include <cstdio>
inline int read(int f = 1, int x = 0, char ch = ' ')
{
    while(!isdigit(ch = getchar())) if(ch == '-') f = -1;
    while(isdigit(ch)) x = x*10+ch-'0', ch = getchar();
    return f*x;
}
const int N = 1e2+5;
int max(int a, int b) { return a>b?a:b; }
int min(int a, int b) { return a<b?a:b; }
short f[N][N][N][N], g[N][N], h[N][N];
char s[N][N];
int n, m, ans, px, py;
int main()
{
    n = read(), m = read(); memset(f, -1, sizeof(f));
    for(int i = 1; i <= n; ++i) scanf("%s", s[i]+1);
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j)
        {
            if(s[i][j] == 'E') px = i, py = j;
            g[i][j] = g[i][j-1]+(s[i][j] == 'o');
            h[i][j] = h[i-1][j]+(s[i][j] == 'o'); 
        }    
    f[0][0][0][0] = 0;    
    int pl = py-1, pr = m-py, pd = px-1, pu = n-px, p;
    for(int l = 0; l <= pl; ++l)
        for(int r = 0; r <= pr; ++r)
            for(int d = 0; d <= pd; ++d)
                for(int u = 0; u <= pu; ++u)
                {
                    if(!(~f[l][r][d][u])) continue;
                    int cl = max(r+1, py-l), cr = min(m-l, py+r);
                    int cd = max(u+1, px-d), cu = min(n-d, px+u);
                    if((p = py+r+1) <= m-l) f[l][r+1][d][u] = max(f[l][r+1][d][u], f[l][r][d][u]+h[cu][p]-h[cd-1][p]);
                    if((p = py-l-1) >= r+1) f[l+1][r][d][u] = max(f[l+1][r][d][u], f[l][r][d][u]+h[cu][p]-h[cd-1][p]);
                    if((p = px+u+1) <= n-d) f[l][r][d][u+1] = max(f[l][r][d][u+1], f[l][r][d][u]+g[p][cr]-g[p][cl-1]);
                    if((p = px-d-1) >= u+1) f[l][r][d+1][u] = max(f[l][r][d+1][u], f[l][r][d][u]+g[p][cr]-g[p][cl-1]);                 
                    ans = max(ans, f[l][r][d][u]);
                }
    printf("%d\n", ans);
    return 0;
}

Namori

给定一个树或基环树，每个点初始是白色，每次操作可以处理一条边，其两个点如果颜色相同则都变成相反的颜色，询问能否将每个点都变为黑色

首先考虑树的情况，考虑对树黑白染色，那么题中的操作就变成了把黑白交换位置，最终黑点变为原来的白点，白点变为原来的黑点，不妨将黑点的权值置为 \(-1\)，白点的权值置为 \(1\)，\(s_x\) 为以 \(x\) 为根的子树的点权和，\(p\) 为根，显然 \(s_p\) 不为 \(0\) 时无解

考虑答案的下界，对于 \(s_x\) 不为 \(0\)，那么 \(x\) 要向父边交换 \(|s_x|\) 个点，则下界为 \(\sum|s_x|\)，这个下界一定可以达到，因为考虑从叶子节点向上按照这样贪心，我们在对 \(x\) 操作前，\(x\) 的子树尽可能满足，即可以找到一个合适的顺序使父边只交换 \(|s_x|\) 个点

再讨论基环树，我们把环上任意一边 \((p,\ q)\) 删掉，首先是奇环，奇环不满足二分图性质，所以断掉的那条边意义与其他边不同，手模几组样例后发现，对这条边的操作可以使得黑白点的差减少 \(2\)，所以当 \(s_p\) 为奇数时问题无解，否则，答案加上 \(|\frac{s_p}{2}|\)，环上所有 \(s_x\) 减 \(\frac{s_p}{2}\) 且 \(s_p\) 自身变为 \(0\)，其次是偶环，偶环满足二分图性质，边的的意义与其他边相同，对环上的交换单独考虑，发现就是一个均分纸牌，求个中位数即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cctype>
using namespace std;
inline int read(int f = 1, int x = 0, char ch = ' ')
{
    while(!isdigit(ch = getchar())) if(ch == '-') f = -1;
    while(isdigit(ch)) x = x*10+ch-'0', ch = getchar();
    return f*x;
}
const int N = 1e5+5;
struct Edge
{
    int next, to;
    Edge(int next = 0, int to = 0):next(next), to(to) {};
}edge[N<<1];
int tot, head[N];
void _add(int x, int y) { edge[++tot] = Edge(head[x], y); head[x] = tot; }
void add(int x, int y) { _add(x, y); _add(y, x); }
int n, m, cn, w[N], f[N], fa[N], s[N], p, q, ans;
int find(int x) { return f[x] == x?x:f[x] = find(f[x]); }
void dfs(int x, int f, int c)
{
    fa[x] = f, s[x] = c;
    for(int i = head[x]; i; i = edge[i].next)
    {
        int y = edge[i].to; if(y == f) continue;
        dfs(y, x, -c); s[x] += s[y];
    }
}
int main()
{
    n = read(), m = read(), p = 1;
    for(int x = 1; x <= n; ++x) f[x] = x;
    for(int i = 1; i <= m; ++i)
    {
        int x = read(), y = read();
        if(find(x) == find(y)) p = x, q = y;
        else f[find(y)] = find(x), add(x, y);
    }
    dfs(p, 0, 1);
    if(n == m)
    {
        for(int x = q; x; x = fa[x]) w[++cn] = s[x];
        if(cn&1)
        {
            if(s[p]&1) return puts("-1"), 0;
            for(int x = q; x; x = fa[x]) s[x] -= s[p]>>1;
        } 
        else
        {
            if(s[p]) return puts("-1"), 0;
            sort(w+1, w+1+cn);   
            for(int x = q; x; x = fa[x]) s[x] -= w[cn>>1];
        }
    }
    else if(s[p]) return puts("-1"), 0;
    for(int x = 1; x <= n; ++x) ans += abs(s[x]);
    printf("%d\n", ans);
    return 0;
}