I'm a first year Computer Science PhD student at the College of AI, Tsinghua University. Before that, I received my Bachelor's degree at the Institute for Interdisciplinary Information Sciences (IIIS), Tsinghua University.
My primary interest of research is on how to build self-improving agents that can learn to interact with the world through trial and error. To achieve this goal, I've been exploring various topics including reinforcement learning, imitation learning, robotics, and generative models.
I am fortunate to be advised by Professor Huazhe(Harry) Xu. I also have the honor to collaborate with and learn from with Professor Xiaolong Wang during my visit at UC San Diego.
Research
Chenhao Lu*,
Xuxin Cheng*,
Jialong Li*,
Shiqi Yang,
Mazeyu Ji,
Chengjing Yuan,
Ge Yang,
Sha Yi,
Xiaolong Wang
International Conference on Robotics and Automation (ICRA) 2024
Website •
ArXiv •
Twitter •
Video •
Code
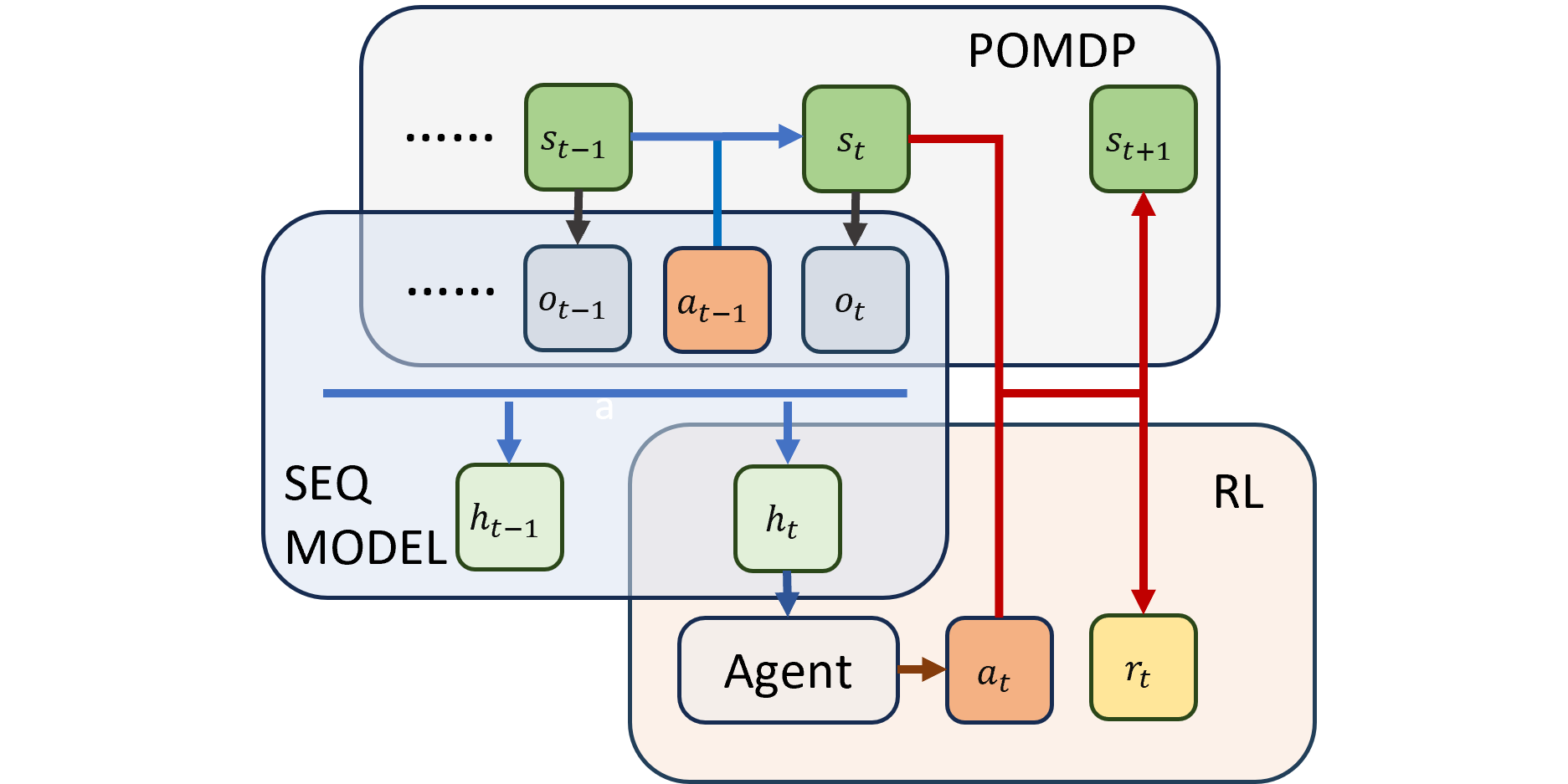Rethinking Transformers in Solving POMDPs
Chenhao Lu,
Ruizhe Shi*,
Yuyao Liu*,
Kaizhe Hu,
Simon Shaolei Du,
Huazhe Xu
The International Conference on Machine Learning (ICML) 2024, Poster
ArXiv •
Code