CTime_Pup_314

不能再颓废了

0%

后缀数组十三题

发表于 更新于 分类于 阅读次数： Valine：
由于蒟蒻的分组导致多个字符串有个可能需要特判只有1个情况
本文也会出现大量口胡，请见谅

蒟蒻的字符串太差了(ಥ _ ಥ)

蒟蒻这辈子再也学不会了≡(▔﹏▔)≡

P2743 [USACO5.1]乐曲主题Musical Themes

题面描述

求不重叠的最长重复子串，其中两个字符串相等的条件变为相同位置两字符差值一定

题解

首先，我们需要解决被重新定义的匹配的问题，相同位置字符差值一定，那么同一个字符串相邻差值与另一个位置的差值相等 例如： \[1\quad 2\quad 3\quad 5 \\\\ 3\quad 4\quad 5\quad 2\] 两个字符串转成差分后变为

\[1\quad 1\quad\ 2 \\\\ 1\quad 1\quad \text{-3}\] 那么 1 2 3 与 3 4 5 相等， 就可以由 1 1 与 1 1 相等得出

即问题变为在差分数组下求原定义的相等的不重叠最大子串，需注意的是差分数组的子串长度+1才是原子串

其次，我们要知道，最大重复子串即为height数组里的最大值，这不难证明，因为重复子串必定是任意两后缀的LCP，而LCP就对应的是height数组一段连续区间的最小值，必定小于等于height的最大值

而现在题目要求不重叠，对长度k进行二分，将问题变为判定长为k的不重叠重复子串的存在问题

所以我们把height值大于等于k的归在一组，只有这样才存在至少长为k的不重叠子串，该组内sa的最大值与最小值的差若小于等于k，就存在

按height分组是常见方法，如图

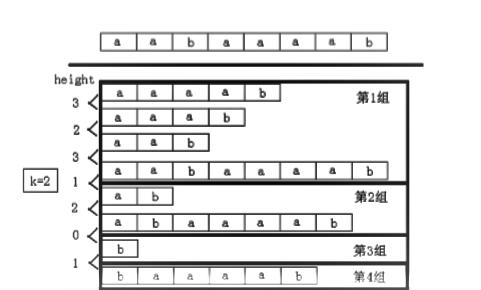
按height分组

实现格式较固定

1
2
3
4
5
6
7
for(int i = 1; i <= n; ++i)
{        
    if(height[i] < k) maxv = -INF, minv = INF;// 重新更新 
    // 每一组内维护的信息
    // 判断是否合法
}

因此第一道题就解决了

差分转化

1
2
3
n = read();
for(int i = 1; i <= n; ++i) a[i] = read();
for(int i = 1; i <= n; ++i) s[i] = a[i]-a[i-1]+100; // 防止负数

判断二分答案合法

1
2
3
4
5
6
7
8
9
10
11
12
bool valid(int k)
{
    int maxv = -INF, minv = INF;
    for(int i = 1; i <= n; ++i)
    {        
        if(height[i] < k) maxv = -INF, minv = INF;        
        maxv = max(sa[i], maxv);
        minv = min(sa[i], minv);
        if(maxv-minv > k) return true; //注意为小于k，因为这是差分数组
    }
    return false;
}

二分答案

1
2
3
4
5
6
7
8
9
10
int l = 0, r = n;
while(l <= r)
{
    int mid = (l+r)>>1;
    if(valid(mid)) l = mid+1, ans = mid;
    else r = mid-1;
}
++ans;
if(ans < 5) ans = 0; // 按题意判断
printf("%d\n", ans);

P2852 [USACO06DEC]牛奶模式Milk Patterns

题面描述

求至少出现k次的最长重复子串

题解

同样，我们发现答案具有单调性，因此问题变为在字符串中判定长度为m的重复子串是否出现k次，height分组后每一组重复子串为这些后缀的公共前缀，那么有多少个后缀就有子串就重复了多少次，若存在一组后缀个数大于k那么m是合法解

判断二分答案

1
2
3
4
5
6
7
8
9
10
bool valid(int k)
{
    int cnt = 0;
    for(int i = 1; i <= n; ++i)
    {
        if(height[i] < k) cnt = 0;
        if(++cnt >= tot) return true; // 子串重复次数即为组的大小
    }
    return false;
}

SP694 DISUBSTR - Distinct Substrings

题面描述

求本质不同的子串个数

题解

每一个后缀的一段前缀就对应了一个子串，我们枚举排名i会产生n-sa[i]+1，由于本质不同，需要减去和已经枚举重复的，即实际贡献n-sa[i]+1-height[i]，注意只需要减与上一个后缀的LCP，因为更前面的实际上已包含在该LCP里了

其次，SPOJ不支持swap(x, y)，所以有些改动

不需要浪费变量名了ヾ(≧▽≦*)o

不开long long 见祖宗

累积答案

1
2
for(int i = 1; i <= n; ++i)
    ans += n-sa[i]+1-height[i];

URAL1297 Palindrome

题面描述

求一个字符串的最大回文子串

题解

把正串和反串拼在一起，枚举对称轴，问题就转化为新字符串中某两个后缀的LCP，长度要用奇偶性分类讨论

查询LCP

1
2
3
4
5
6
7
int LCP(int i, int j) // 查询位置为i和j的后缀的LCP
{
    int l = rak[i], r = rak[j];
    if(l > r) swap(l, r); ++l;
    int k = log2(r-l+1);
    return min(f[l][k], f[r-(1<<k)+1][k]); // f为喜闻乐见的ST表
}

合并正反两串

1
2
3
4
scanf("%s", s+1); len = strlen(s+1); n = 2*len+1;
for(int i = 1; i <= len; ++i) 
    s[n+1-i] = s[i];
s[len+1] = 1; // 放置特殊特殊节点，最好是1，其他由于数据类型的原因会有奇怪错误

这种写法较麻烦，后文有更普适的

奇偶分类讨论，画图模拟即可

奇偶分类 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
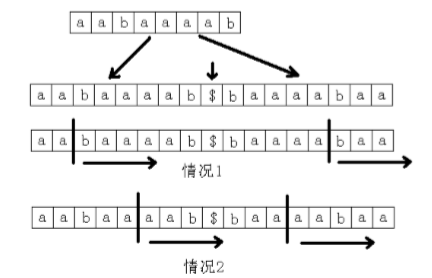
for(int i = 1; i <= len; ++i)
{
    int cur = LCP(i, n+1-i);
    if(2*cur-1 > ans)
    {
        ans = 2*cur-1;
        pos1 = i-cur+1;
        pos2 = i+cur-1;
    }
    if(i < 2) continue;       
    cur = LCP(i, n+2-i);
    if(2*cur > ans)
    {
        ans = 2*cur;
        pos1 = i-cur;
        pos2 = i+cur-1;
    }
}

UVA10298 Power Strings

题面描述

求循环同构串的最小循环节

题解

蒟蒻连KMP都不会写了 (～﹃～)~zZ

枚举长度的约数，假设枚举值为k，即查找位置为1与位置为k+1的后缀的LCP是否为n-k即可

画图感性理解

枚举过程

1
2
for(int k = 1; k < n; ++k)
    if(n%k == 0 && LCP(1, k+1) == n-k) ans = n/k, k = n;

POJ3693 Maximum repetition substring

题面描述

求一个字符串的循环次数最多的循环同构子串，其次满足字典序最小

题解

蒟蒻调了好久，还是网上抄的的题解 ◑﹏◐

但是这确实是一道好题 o(￣▽￣)o

首先，这道题和上一道类似，我们可以考虑枚举循环节的长度，同时枚举每一个位置，假设当前枚举的位置为j，长度i，则计算j和i+j的LCP，那么这个循环同构子串循环为LCP/i+1，更新答案和位置即可

但是时间复杂度为O(n^2)，显然过不了，考虑优化

对于长度i的循环节，如果只枚举S(1, i), S(i+1, i*2+1) ... 会发生什么，我们会漏记循环次数，但此时它一定是一个更多循环次数子串的后缀，所以我们再向前寻找i个即可，向前匹配了LCP%i个字符循环次数+1

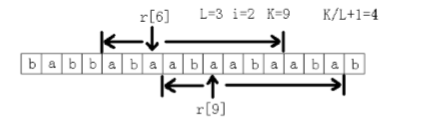
寻找循环同构子串

但时间复杂度不太会算啊（；´д｀）ゞ ， 感性上，均摊和随机都比较优秀，大概是O(nlogn+k)，k是一个与n无关的常数

1
2
3
4
5
6
7
8
9
10
11
for(int i = 1; i <= n/2; ++i) // 枚举到n/2即可
    for(int j = 1; j+i <= n; j += i)
    {
        if(s[j] != s[j+i]) continue;
        int lcp = LCP(j, j+i);
        int curr = lcp/i+1, exl = j-(i-lcp%i), curl = j, cnt = 0; // curr 重复次数，exl 匹配到这个位置curr+1
        for(int k = j-1; k > j-i&&k&&s[k] == s[i+k]; --k) // 如果不大于exl则重复次数增加，但还会继续枚举
        {
            if(exl == k) ++curr, curl = k;
        }
    }

接下来，我们考虑字典序最小

暴力统计，我们考虑rank数组，通过rank[i] 和 rank[j] 我们可以比较任意两个后缀的排名，而子串一定是某个后缀的前缀，对于完全不同的子串，若首字符位置不同，我们可以通过直接比较后缀即可，若位置相同，就比较长度，对于完全相同的子串，细节留给读者思考

1
2
3
4
5
6
7
8
9
10
11
12
13
14
for(int i = 1; i <= n/2; ++i)
    for(int j = 1; j+i <= n; j += i)
    {
        if(s[j] != s[j+i]) continue;
        int lcp = LCP(j, j+i);
        int curr = lcp/i+1, exl = j-(i-lcp%i), curl = j, cnt = 0;
        for(int k = j-1; k > j-i&&k&&s[k] == s[i+k]; --k)
        {
            if(exl == k) ++curr, curl = k;
            else curl = rak[k]< rak[curl]?k:curl; // 时刻更新首字符
        }
        if(curr > maxr) maxr = curr, len = i, p = curl;
        else if(curr == maxr && rak[curl] < rak[p]) maxr = curr, len = i, p = curl; // 按照长度枚举rank相同先枚举的字典序大
    }

POJ2274 Long Long Message

题面描述

求两个字符串的最长公共子串

题解

两个字符串的最长公共子串必定是两个字符串任意两个后缀的最长公共前缀，我们把两个字符串拼在一起，从中取满足sa[i-1] 和 sa[i] 分别属于两个字符串的height的最大值

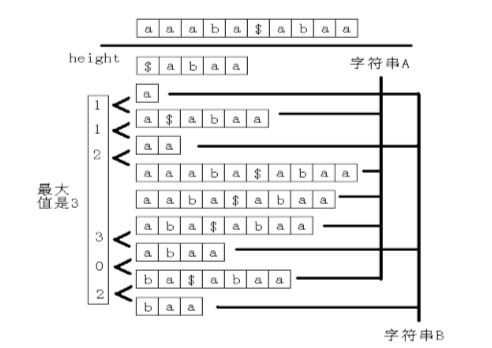
拼接后的SA数组 
1
2
3
for(int i = 2; i <= n; ++i)
    if((sa[i] < p && sa[i-1] > p) || (sa[i] > p&&sa[i-1] < p))
        ans = max(ans, height[i]);

之后会更改判断子串位置的写法

POJ3415 Common Substrings

题面描述

求两个字符串长度不小于 k 的公共子串的个数（可以相同）

题解

好题 ヾ(≧▽≦*)o

那一刻我仿佛会了单调栈

题意可以转化为，我们定义

\[A(i,\ k)\]

表示字符串A从第i个位置开始长度为k的子串

定义集合

\[S = \{(i,\ j,\ k)\ |\ K \le k,\ A(i,\ k) = B(j,\ k) \}\]

代表公共子串集合，题目实际上就是求\(|S|\)

那么

\[|S|\ = \sum_{i=1}\sum_{j=1}\sum_{k=1}[A(i,\ k)==B(j,\ k)][K \le k]\]

\[=\sum_{i=1}\sum_{j=1}LCP(i,\ j)-K+1[K \le k]\ \]

所以，我们把两个字符串拼在一起，按照\(height\)分组，先考虑枚举A的子串S，求出字典序比S小的B的子串\(LCP-K+1\)的总和，然后在反过来枚举B的子串，相当于把大于A的子串字典序的贡献计算一遍，就得到了\(|S|\)

相当于对于枚举A的位置i来说它的贡献为

\[\sum_{j<i}\min_{k=j}^{i}(height_k)-K+1[sa[j-1]\in B]\ [sa[i] \in A]\]

很显然 \(\min_{k=j}^{i}(height_k)\) 具有单调性，对于\(j'\)<\(j\)，就有 \(\min_{k=j}^{i}(height_k)\le\min_{k=j'}^{i}(height_k)\)，并且当\(i\ \rightarrow i+1\)时，决策集合靠后的可能会变小

所以，我们可以用一个单调栈维护\(height\)和\(cnt\)，当一个新的决策入栈后，把若\(height_{top} \ge height_i\)弹出栈顶，并更新具有相同\(height\)的\(cnt\)

具体来说

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int top = 0; // 枚举B，计算A
ll sum = 0;
for(int i = 1; i <= n; ++i)
{
    if(height[i] < len) { sum = top = 0; continue; } // 和之前分组不同的是height是主要决策，当这一个height不满足时直接跳过
    int cnt = 0;
    if(bel[sa[i-1]] == 1) ++cnt, sum += height[i]-len+1; // 假如是上一个后缀是Aheight更新贡献
    while(top&&stak[top][0] >= height[i])
        sum -= stak[top][1]*(stak[top][0]-height[i]),
        cnt += stak[top][1],
        --top; // 维护单调性
    stak[++top][0] = height[i]; stak[top][1] = cnt;
    if(bel[sa[i]] == 2) ans += sum; // 如果是B串累计贡献
}

POJ3294 Life Forms

题面描述

求不小于k个字符串中的最长子串

题解

把字符串拼在一起，中间用特殊字符隔开

1
2
3
4
5
6
for(int k = 1; k <= tot; ++k)
{
    scanf("%s", inps+1);
    for(int i = 1; inps[i]; ++i) s[++n] = inps[i], bel[n] = k;
    s[++n] = (++spc)+S; bel[n] = k;
}

这是合并字符串的最终版本，s是int类型的，S是字符集大小

二分长度，判断每组内是否有k个不同的字符串

1
2
3
4
5
6
7
8
9
10
11
12
bool valid(int k)
{
    int t = 0;
    for(int i = 1; i <= n; ++i)
    {
        if(height[i] < k) for(int j = 1; j <= tot; ++j) t = cnt[j] = 0;
        int x = bel[sa[i]];
        if(x && ++cnt[x] == 1) ++t;
        if(t >= tot/2+1) return true;
    }
    return false;
}

再把满足条件的最大长度，来统计字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
int getAns(int k)
{
    if(!k) return 0;
    int t = 0, ta = 0, tag = 0;
    for(int i = 1; i <= n; ++i)
    {
        if(height[i] < k) for(int j = 1; j <= tot; ++j) tag = t = cnt[j] = 0;
        int x = bel[sa[i]];
        if(x && ++cnt[x] == 1) ++t;
        if(t == tot/2+1 && !tag) ans[++ta] = sa[i], tag = 1;
    }
    return ta;
}

输出格式有锅 ㄟ( ▔, ▔ )ㄏ

SP220 PHRASES - Relevant Phrases of Annihilation

题面描述

求每个字符串至少出现两次且不重叠的最长子串

题解

前面几道题的综合，拼在一起，二分，统计每组不同串的个数，用相同串的\(sa_{max}-sa_{min}\)是否大于二分值即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool valid(int k)
{
    for(int x = 1; x <= tot; ++x) cnt[x] = 0, maxv[x] = -1, minv[x] = n;
    for(int i = 1; i <= n; ++i)
    {
        if(height[i] < k) 
        {
            bool cor = true;
            for(int x = 1; x <= tot && cor; ++x)
                if(cnt[x] < 2) cor = false;
                else if(maxv[x]-minv[x] < k) cor = false;
            if(cor) return true;
            for(int x = 1; x <= tot; ++x) cnt[x] = 0, maxv[x] = -1, minv[x] = n;
        }
        int x = bel[sa[i]];
        ++cnt[x]; 
        maxv[x] = max(maxv[x], sa[i]);
        minv[x] = min(minv[x], sa[i]);
    }
    return false;
}

POJ1226 Substrings

题面描述

求出现或反转后出现在每个字符串中的最长子串

题解

正串反串拼一块，所有串拼一块，二分即可

拼串

1
2
3
4
5
6
7
8
9
for(int k = 1; k <= tot; ++k)
{
    scanf("%s", inps+1);
    int strl = strlen(inps+1);
    for(int i = 1; i <= strl; ++i) s[++n] = inps[i], bel[n] = k;
    s[++n] = (++spc)+128; bel[n] = k;
    for(int i = strl; i; --i) s[++n] = inps[i], bel[n] = k;
    s[++n] = (++spc)+128; bel[n] = k;
}

完结散花ヾ(•ω•`)o

SA真是人类的智慧

可是蒟蒻还是不会字符串啊

参考论文 后缀数组——处理字符串的有力工具