ZYB和售货机
题面描述
基环内向树森林，每个点有一个容量和权值，每次可以选择一个容量不为
\(0\)
的点把它的出点容量减少，答案增加减少量乘点权，最大化收益
题解
由题意知，\((i,\ f_i)\)
构成的边集和所给点集构成了基环内向树森林
基环内向树即使有且仅有一个有向环，且所有点出度为 \(1\) 的树形图
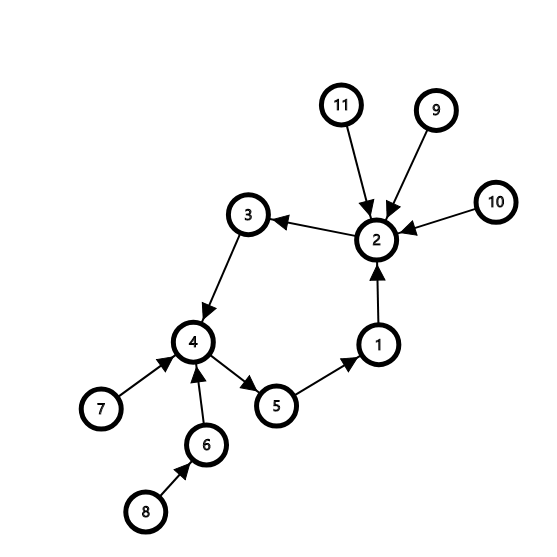稍加思考我们可以发现对于每一个非叶节点的容量都可以通过找连向它的点权最大值来配对直到容量变为
\(1\)
并且通过每个节点找连向它的节点的最大值这样的构造使树形图分割成若干个有向链和不超过
\(1\) 个的有向环
并且在这种构造下，每个点的入度和出度都不超过 \(1\) 所以一定不相交
而且如果存在环，一定是基环树的环
像这样
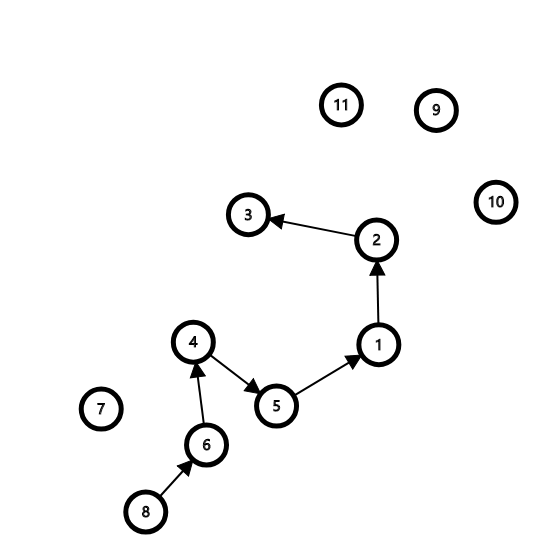只有链
或这样
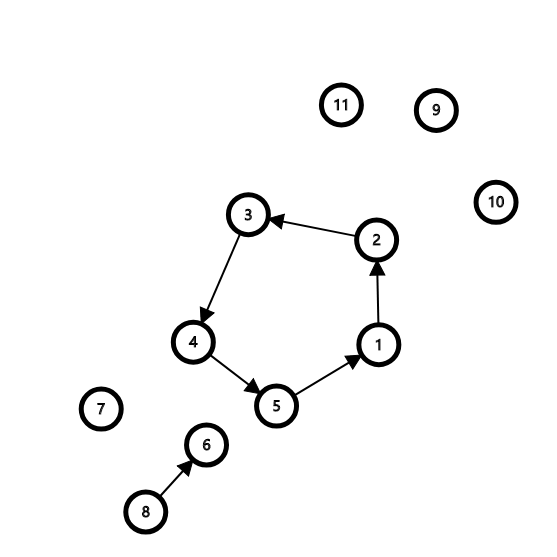有链和环
对于链而言，我们从出度为 \(0\)
的点一直选下去就是合法的
对于环而言，我们必须断掉一个环边换成树边，所以我们必须找到一个最大值和次大值差最小的点
断环加边不会出现新的环，因为基环树只有一个环
对于上一张图，需要这样断
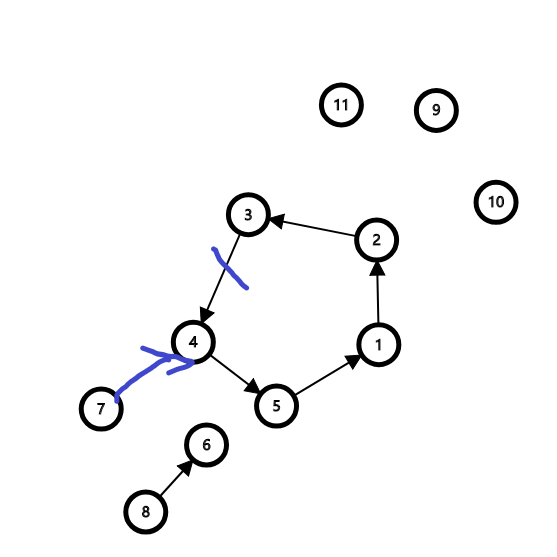断环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| #include <cstdio>
#include <algorithm>
#include <cstring>
#include <cctype>
using namespace std;
typedef long long int64;
inline int read(int f = 1, int x = 0, char ch = ' ')
{
while(!isdigit(ch = getchar())) if(ch == '-') f = -1;
while(isdigit(ch)) x = x*10+ch-'0', ch = getchar();
return f*x;
}
const int N = 1e5+5, INF = 0x3f3f3f3f;
int n, f[N], c[N], d[N], a[N];
int col[N], w[N], fm[N], sm[N], mind;
int64 ans;
void dfs(int x, int p)
{
if(col[x] == p)
{
ans -= mind;
return;
}
else if(col[x]) return;
col[x] = p;
if(!fm[x]) return;
ans += 1ll*w[fm[x]]*a[x];
mind = min(mind, w[fm[x]]-w[sm[x]]);
if(fm[x] != x) dfs(fm[x], p);
}
int main()
{
freopen("goods.in", "r", stdin);
freopen("goods.out", "w", stdout);
n = read();
for(int x = 1; x <= n; ++x) f[x] = read(), c[x] = read(), d[x] = read(), a[x] = read();
for(int x = 1; x <= n; ++x)
{
w[x] = d[f[x]]-c[x];
if(w[x] > w[fm[f[x]]]) sm[f[x]] = fm[f[x]], fm[f[x]] = x;
else if(w[x] > w[sm[f[x]]]) sm[f[x]] = x;
}
for(int x = 1; x <= n; ++x)
if(!col[x]) mind = INF, dfs(x, x);
printf("%lld\n", ans);
return 0;
}
|
ZYB玩字符串
给定字符串并已知该字符串是由若干个原串按顺序离散后重组成的，求出长度最小且字典序最小原串
我们考虑判断一个串是否合法的过程，发现如果按从左向右的顺序依次考虑则对于
\([l,\ r]\) 来说以合法地删去若干原串
\(p\) 后剩下的部分一定是 \(p\) 的前缀
考虑状态 \(f_{l,r}\) 表示 \([l,\ r]\) 合法地删去若干原串后是否为 \(p\) 的前缀，并且当 \(l_p|r-l+1\) 时 \([l,\ r]\) 恰好被 \(p\) 删完
所以考虑 \(f_{l,r}\)
如何转移出去
首先可以在 \(f_{l,r}\)
后匹配当前前缀的下一个字符
\[
\begin{aligned}
f_{l,r+1}\ =\ f_{l,r}\ \&\ [\ s[r+1]\ ==\ p[(r-l+1)\ mod\ l_p+1]\ ]
\end{aligned}
\]
其次可以在 \(f_{l,r}\)
后加上一个合法的恰好被完全删完的区间
\[
\begin{aligned}
f_{l,r+k\times l_p}\ =\ f_{l,r}\ \&\ f_{r+1,r+k\times l_p}
\end{aligned}
\]
我们把刷表改成填表差不多就是一个常规的区间 \(DP\) 了
注意微小的剪枝即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| #include <cstring>
#include <algorithm>
#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;
const int N = 2e2+5;
int t, n;
string s, p;
vector<string> ans;
int f[N][N];
int c[N];
bool dfs(int l, int r, int lp)
{
if(~f[l][r]) return f[l][r];
if(l == r) return f[l][r] = p[1] == s[l];
for(int k = 1; l <= r-k*lp; ++k)
if(dfs(l, r-k*lp, lp)&&dfs(r-k*lp+1, r, lp))
return f[l][r] = 1;
if(s[r] == p[(r-l)%lp+1]) return f[l][r] = dfs(l, r-1, lp);
else return f[l][r] = 0;
}
bool valid(int lp)
{
memset(f, -1, sizeof(f));
for(int i = 'a'; i <= 'z'; ++i) c[i] = 0;
for(int i = 1; i <= lp; ++i) ++c[p[i]];
for(int i = 1; i <= n; ++i) if(!c[s[i]]) return false;
return dfs(1, n, lp);
}
int main()
{
freopen("string.in", "r", stdin);
freopen("string.out", "w", stdout);
cin>>t;
while(t--)
{
cin>>s; n = s.length(); s = ' '+s; ans.clear();
for(int lp = 1; lp <= n&&ans.empty(); ++lp)
{
if(n%lp) continue;
for(int i = 1; i <= n-lp+1; ++i)
{
p = s.substr(i, lp); p = ' '+p;
if(valid(lp)) ans.push_back(s.substr(i, lp));
}
}
sort(ans.begin(), ans.end());
cout<<ans[0]<<endl;
}
return 0;
}
|