CTime_Pup_314

不能再颓废了

0%

永远学不会的Miller–Rabin和Pollard-Rho算法

发表于 更新于 分类于 阅读次数： Valine：

下文未特殊说明则使用 \(p\) 代表素数, \(n\) 代表自然数

Miller-Rabin素性检验

前置知识

费马小定理

费马小定理的一般表述为

\[ \begin{aligned} a^{p-1}\ \equiv\ 1\ (\ mod\ p\ ),\ \forall\ a \in \mathbb{N},\ (a,\ p)\ =\ 1 \end{aligned} \] 然而遗憾的是费马小定理的逆命题并不成立，也就是

\[ \begin{aligned} a^{n-1}\ \equiv\ 1\ (\ mod\ n\ ),\ \exists\ a \in \mathbb{N},\ \,(a,\ p)\ =\ 1 \nRightarrow n \in\ P \end{aligned} \]

尤其是对于一类强伪素数 \(Carmichael\) 数 恰好能满足能满足费马小定理，例如 \(561\)

因此，仅使用费马小定理逆命题进行素性检验喜闻乐见的失败了

然而幸运的是，费马小定理存在逆否定理，我们可以据此给素性判定提供证据

二次探测

再用费马小定理进行素性检验失败后，我们注意到一个十分有趣的引理

\[ \begin{aligned} \forall p,\ x^2\ \equiv\ 1\ (\ mod\ p)\ \Rightarrow x_1\ =\ -1,\ x_2\ =\ 1 \end{aligned} \]

我们把 \(-1,\ 1\) 称作 \(1\ mod\ p\) 的平凡平方根

并且，对于 \(p\) 而言不存在非凡平凡根

下面给出一个简短的证明

设 \(1\ mod\ p\) 存在非凡平方根 \(x\) 满足 \(x\ \ne 1,\ x\ \ne\ -1\)

\(\because\ x^2\ \equiv\ 1\ (\ mod\ p)\ \therefore\ (x-1)(x+1)\ \equiv\ 0\ (\ mod\ p)\)

\(\because(x-1)\perp(x+1)\ \therefore\ p\ |\ (x-1)\) 或 \(p\ |\ (x+1)\)

与假设矛盾，所以不成立

我们就可以提供另一类强伪证

算法内容

具体来说，我们对 \(n\) 进行素性检测时

若 \(n\) 为偶数，则可以直接提供证据

若 \(n\) 为奇数，则有 \(n-1\ =\ 2^tr\)

我们设 \(x_k\ =\ x^{2^kt}\) 则有 \(x_k\ =\ x_{k-1}^2\)

根据上述引理当 \(x_k\ \equiv\ 1\ (\ mod\ n)\) 我们只需验证 \(x_{k-1}\) 是否为 \(1\) 或 \(-1\) 就可以提供证据

同时，通过最后的 \(x^{n-1}\ mod\ p\) 的值使用费马小定理的逆否定理再此提供证据

也就是说我们选择足够多的 \(x\) 就可以通过这些强伪证得出 \(n\) 时否为质数的结论

假设 \(k\) 为试验次数，出错概率 \(P\ =\ 4^{-k}\)

而事实上，对于算法竞赛的常见数据范围，我们可以通过一些特定的 \(x\) 判断，如图

x的选取

一般来说，前 \(12\) 个质数即可

P3383 [模板]线性筛素数素性检测

虽然这是线筛的板子，但是 \(Miller-Robin\) 素性检验明显由于线筛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cctype>
using namespace std;
typedef long long int64;
inline int read(int f = 1, int x = 0, char ch = ' ')
{
    while(!isdigit(ch = getchar())) if(ch == '-') f = -1;
    while(isdigit(ch)) x = x*10+ch-'0', ch = getchar();
    return f*x;
}
const int p[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37}; // 前12个质数即可
int qpow(int a, int b, int n)
{
    int ret = 1;
    for( ; b; b >>= 1, a = 1ll*a*a%n) if(b&1) ret = 1ll*ret*a%n;
    return ret;
}
bool miller_rabin(int64 n)
{
    if(n == 1) return false;
    for(int i = 0; i < 12; ++i) if(n%p[i] == 0) return n == p[i]; // 整除直接判断
    int64 r, x, y; int t;
    for(r = n-1, t = 0; ~r&1; r >>= 1, ++t); // n = r*2^t
    for(int i = 0; i < 12; ++i)
    {
        x = qpow(p[i], r, n);
        for(int j = 1; j <= t; ++j) // 二次探测
        {            
            y = 1ll*x*x%n;
            if(y == 1&&x != n-1&&x != 1) return false; // 确定一定为合数
            x = y;
        }
        if(x != 1) return false; // 费马小定理逆否定理确定为合数
    }
    return true; // 通过这些强伪证证明是素数
}
int t, n;
int main()
{
    n = read(); t = read();
    while(t--)
    {
        n = read();
        if(miller_rabin(n)) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

Pollard-Rho算法

前置知识

生日悖论

在一个房间里需要有 \(23\) 人使两个人生日相同的概率超过 \(50\%\)

在一个房间里需要有 \(64\) 使人两个人生日相同的概率接近 \(1\)

所以，这种组合随机抽样的方式有很高的概率出现相同

由于这个问题与常识不相同，所以被叫做生日悖论

Floyd判圈算法

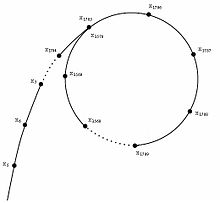
假设序列 \(\{x_k\}\) 再 \(x_u\) 之后出现长度为 \(v\) 的循环，既满足 \(x_{u+v}\ =\ x_u\)，考虑龟兔赛跑的过程，我们让一个指针走的快，另一个指针走的慢，最后一定会的相遇而此时周期即为时间 \(t\)

算法演示
判圈算法

算法内容

考虑 \(n\ =\ ab\) 其中 \(a,\ b\) 是 \(n\) 的非平凡因子，即 \(a,\ b\ \ne\ 1,\ n\) 且 \(a,\ b\ |\ n\)

我们如果单纯随机 \(a\) 是不可能的

我们注意到如果 \(x-y\ |\ a\) 和 \(x-y\ \nmid n\) 那么 \(a\ =\ (x-y,\ n)\)

所以，我们可以随机选择不相等的 \(x\) 和 \(y\) 的算出 \(a\) 而且我们只需随机 \(O(n^{\frac{1}{4}})\) 组即可 关键是如何选出不相等的和如何储存大量随机数

考虑模 \(n\) 意义下随机多项式 \(g(x)\ \equiv\ x^2+c\ (mod\ n)\) 生成伪随机数列 \(\{x_k\}\)

但由于 \(\{x_k\}\) 是 \(n\) 的剩余系，所以是有限的

因此根据生日悖论 \(O(\sqrt{n})\) 的期望下我们可以找到一个相同的 \(x\) 和 \(y\) 之后出现周期，实现即使用 \(Floyd\) 判圈算法，而在出现环前我们有极大可能找到了非平凡因子，否则就更换参数 \(c\) 重新寻找

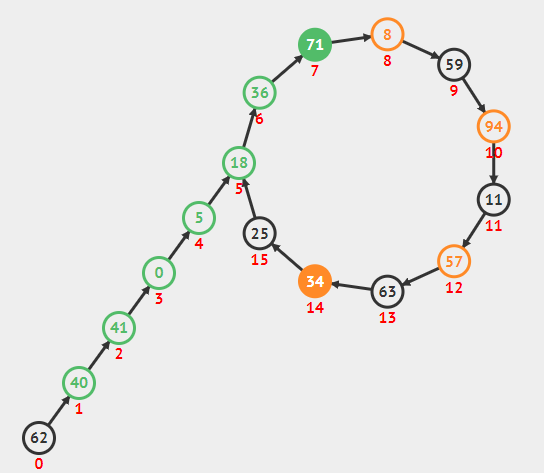
这个过程就像走希腊字母 \(\rho\) 路径因此得名

Rho的来历

P4718 [模板]Pollard-Rho算法

Pollar-Rho板子题

按照上述口胡

我们大致写出程序主体，但事实上发现喜闻乐见的 \(TLE\) 了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
uint64 func(uint64 x, uint64 c, uint64 n) { return ((int128)x*x%n+c)%n; }
uint64 find(uint64 n)
{
    for(int i = 0; i < 12; ++i) if(n%p[i] == 0) return p[i]; // 用12个质数判一下，小数据不能达到期望
    int s = 0, c = rand(); uint64 x, y;
    x = y = func(rand(), c, n);
    do
    {
        uint64 d = gcd((x-y+n)%n, n); // 验证是否为非平凡因子
        if(d != 1&&d != n) return d;
        x = func(x, c, n); y = func(func(y, c, n), c, n); ++s; // floyd 判圈
    } while(x != y&&s <= S);
    return 0;
}
void pollar_rho(uint64 n, uint64 &mfact)
{
    if(n <= mfact) return;
    while(~n&1) n >>= 1, mfact = max(mfact, (uint64)2);
    if(n == 1||miller_robin(n)) return void(mfact = max(mfact, n));
    uint64 d = find(n); for( ; !d; d = find(n));
    d = max(d, n/d); // 继续分解
    pollar_rho(d, mfact); pollar_rho(n/d, mfact); 
}

以下是我也看不懂，但感觉很有道理的优化

\(TLE\) 的瓶颈在于 \(gcd\) 的多次计算

考虑 \(gcd(ac,\ b) = gcd(a, b)\)，我们可以把多个 \(gcd\) 一起计算

同时使用倍增的思想依次增大样本集合，每次选择组大小一定的 \(x, y\) 一起计算

目的是达到不再环上停留同时优化 \(gcd\)

至于组的大小，\(wiki\) 上是 \(100\)，\(zzt\) 是 \(512\)，也有人是 \(127\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
uint64 find(uint64 n)
{
    for(int i = 0; i < 12; ++i) if(n%p[i] == 0) return p[i];
    int c = rand(); uint64 y = rand(), x = y, z, g;
    for(int s = 1; ; s <<= 1, x = y)
    {
        for(int k = 1; k <= s; k += S) // 一组一组的算
        {
            int t = min(S, s-k); g = 1, z = y;
            for(int i = 1; i <= t; ++i) y = f(y), g = (int128)g*(y-x+n)%n;
            g = gcd(g, n);
            if(g == 1) continue;
            if(g == n) for(g = 1, y = z; g == 1; ) y = f(y), g = gcd(y-x+n, n); // 若最大公约数不为 1 则出现了 大于 1的因子
            return g;
        }
    }
}

完整代码 数据类型转换过于毒瘤

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <cstdio>
#include <cstring>
#include <cctype>
#include <cstdlib>
#include <algorithm>
#define f(x) ((int128)x*x+c)%n
using namespace std;
typedef unsigned long long uint64;
typedef __int128 int128;
inline uint64 read(int f = 1, uint64 x = 0, char ch = ' ')
{   
    while(!isdigit(ch = getchar())) if(ch == '-') f = -1;
    while(isdigit(ch)) x = x*10+ch-'0', ch = getchar();
    return f*x;
}
const int p[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37}, S = 127;
uint64 qpow(uint64 a, uint64 b, uint64 n)
{
    uint64 ret = 1;
    for( ; b; b >>= 1, a = (int128)a*a%n) if(b&1) ret = (int128)ret*a%n;
    return ret;
}
uint64 gcd(uint64 a, uint64 b) { return b?gcd(b, a%b):a; }
bool miller_robin(uint64 n)
{   
    if(n == 1) return false;
    for(int i = 0; i < 12; ++i) if(n%p[i] == 0) return n == p[i];
    uint64 r; int t;
    for(r = n-1, t = 0; ~r&1; r >>= 1, ++t);
    for(int i = 0; i < 12; ++i)
    {
        uint64 x = qpow(p[i], r, n), xs;
        for(int j = 1; j <= t; ++j)
        {
            xs = (int128)x*x%n;
            if(xs == 1&&x != 1&&x != n-1) return false;
            x = xs;
        }
        if(x != 1) return false;
    }
    return true;
}
uint64 find(uint64 n)
{
    for(int i = 0; i < 12; ++i) if(n%p[i] == 0) return p[i];
    int c = rand(); uint64 y = rand(), x = y, z, g;
    for(int s = 1; ; s <<= 1, x = y)
    {
        for(int i = 1; i <= s; ++i) y = f(y);
        for(int k = 1; k <= s; k += S)
        {
            int t = min(S, s-k); g = 1, z = y;
            for(int i = 1; i <= t; ++i) y = f(y), g = (int128)g*(y-x+n)%n;
            g = gcd(g, n);
            if(g == 1) continue;
            if(g == n) for(g = 1, y = z; g == 1; ) y = f(y), g = gcd(y-x+n, n);
            return g;
        }
    }
}
void pollard_rho(uint64 n, uint64 &mfact)
{
    if(n <= mfact) return;
    while(~n&1) n >>= 1, mfact = max(mfact, (uint64)2);
    if(n == 1||miller_robin(n)) return void(mfact = max(mfact, n));
    uint64 d = find(n); for( ; d == n; d = find(n));
    d = max(d, n/d);
    pollar_rho(d, mfact); pollar_rho(n/d, mfact); 
}
int t;
int main()
{
    srand(19260817);
    t = read();
    while(t--)
    {
        uint64 n = read(), m = 0;
        if(miller_robin(n)) puts("Prime");
        else pollar_rho(n, m), printf("%llu\n", m);
    }
    return 0;
}

特别感谢 wikipedia visualgo whzzt LinearOD

资料来源

Pollard Rho 算法简介

Pollard-Rho algorithm

Birthday problem

Pollard's Rho Algorithm

Miller-Rabin primality test