CTime_Pup_314

题面描述

求满足题目中限制条件的合法填数数量

题解

我不会推性质，只好写一个状压得 \(60\) 暴力分

我们发现题目中得状态必须和位置与至于有关，不妨考虑状态 \(f_{i,l,r}\) 代表在位置 \(i\) 取值范围为 \([l,\ r]\) 得方案数，考虑这个状态如何转移出去

题面描述

给定矩阵和多个子矩形权值，对矩阵填数满足给定子矩阵的最大值为权值，求方案数

题解

很容易想到容斥，但是我太菜了不知道怎么算，一直认为补集转换时由等于必须变为不等于，但是却没想到全集是可以自己定义的，这样就可以由等于变为小于了，剩下就比较好办了，离散化后分割矩阵即可

题目描述

求二阶线性常系数齐次递推的平方和。

题解

由于这道题意要求，下文数列下标都从 1 开始

前置知识

线性常系数齐次递推关系

若递推关系满足

\[ f_n\ =\ \sum_{i=1}^kc_if_{n-i}\ (n >k) \]

C

题面描述

树上快速维护位运算

题解

设 \(u\) 和 \(v\) 的有向简单路径构成的集合为 \(S(u,\ v)\) 题意即是求 \[ \sum_{w\in S(u,v)}a_w\ or\ dis(u,\ w) \]

\(dis(u,\ w)\) 表示边数

下文未特殊说明则使用 \(p\) 代表素数, \(n\) 代表自然数

Miller-Rabin素性检验

前置知识

费马小定理

费马小定理的一般表述为

\[ \begin{aligned} a^{p-1}\ \equiv\ 1\ (\ mod\ p\ ),\ \forall\ a \in \mathbb{N},\ (a,\ p)\ =\ 1 \end{aligned} \]

ZYB和售货机

题面描述

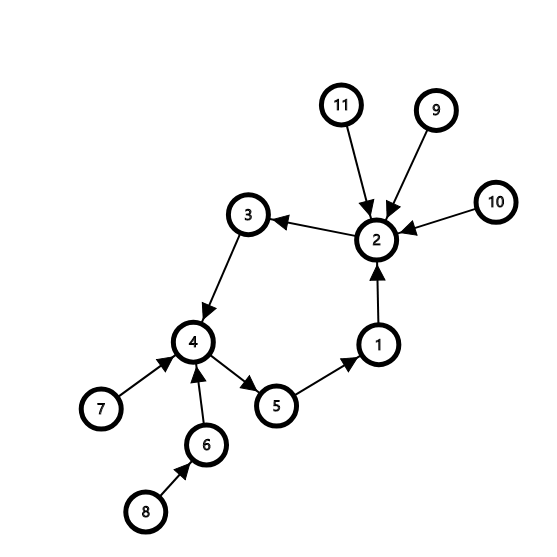
基环内向树森林，每个点有一个容量和权值，每次可以选择一个容量不为 \(0\) 的点把它的出点容量减少，答案增加减少量乘点权，最大化收益

题解

由题意知，\((i,\ f_i)\) 构成的边集和所给点集构成了基环内向树森林

基环内向树即使有且仅有一个有向环，且所有点出度为 \(1\) 的树形图

题面描述

连续和的异或值。

题解

题目实际要求出

\[ \begin{aligned} ans\ =\ \oplus \sum_{i=1}^n\sum_{j=0}^{i-1}sum_i-sum_j \end{aligned} \]

然后，我看了一下二进制加法器后直接弃疗

题面描述

树形图拓扑排序计数

题解

论用一种错误的顺序做三倍经验是一种怎样的体验

题面描述

在棋盘内破坏指定联通块的最小代价

莫比乌斯函数

设 \(x\in N\) 唯一分解后为 \(x\ =\ p_1^{c_1}p_2^{c_2}p_3^{c_3}\cdots p_n^{c_n}\)

我们定义莫比乌斯函数

\[ \mu(x)\ = \ \begin{cases} 0&\exists\ c_i > 1\\\\ -1&n\ \equiv\ 1\ (\ mod\ 2\ )\\\\ 1&n\ \equiv\ 0\ (\mod\ 2\ ) \end{cases} \]